誰もが知っている黄金比率(1:1.618)。デザイナーならこの数値を知っている人も多いと思います。また、フィボナッチ数列というのも知っている方が多いと思いますが、この黄金比率とフィボナッッチ数列は関係しており、その解説をわかりやすく解説します。
フィボナッチ数列とは
フィボナッチ数列は、1202年にイタリアの天才的数学者レオナルド=フィボナッチ(Leonardo Fibonacci、1170年頃 – 1250年頃)によって発見されました。
フィボナッチが考えたのは、つがいのうさぎの増えかたについて。
子うさぎのつがいは1ヶ月でおとなのつがいになり、2ヶ月目から親うさぎになり、毎月つがいの子うさぎを産む。
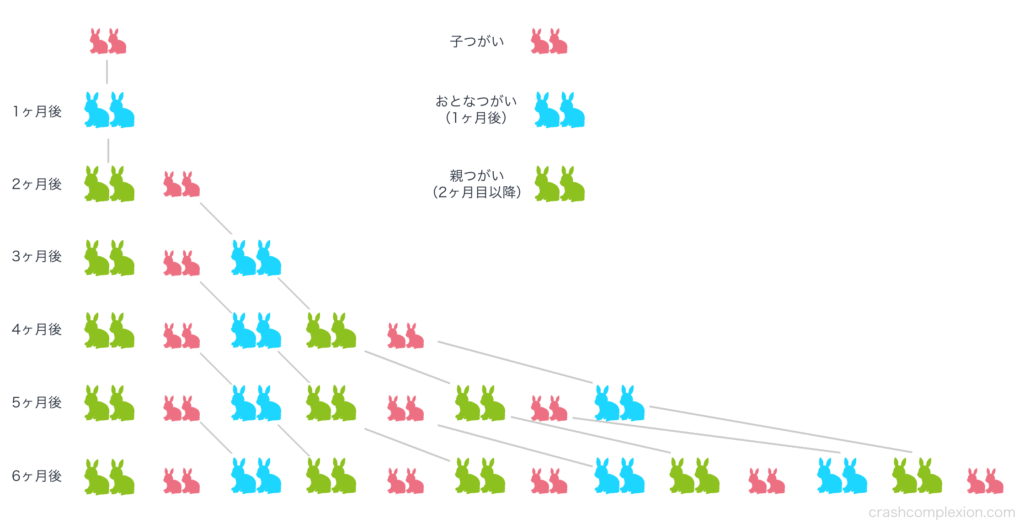
わかりやすく子つがいおとなつがい、親つがいと分けて説明します。
子つがいAは1ヶ月後におとなつがいになる。
2ヶ月目に親つがいになり、子つがいを産む。
3ヶ月目には親つがいはまた子つがいを産み、先月生まれた子つがいはおとなつがいに成長。
4ヶ月目には親つがいはさらに子つがいを産み、先月生まれた子つがいはおとなつがいに成長。さらに先月おとなつがいになったつがいは親つがいになり子つがいを産む。
というような感じである。
こうしたルールに従うと、1、1、2、3、5、8、13、21、34、55、89、144…という数列が見られます。
どの数もその前の2つの数を足し合わせたものになっている。
この数列は自然界にも存在します。
自然界のフィボナッチ数列
植物を観察すると、一見無秩序に見えますが、よく目を凝らすと、数や形の法則が隠されています。
以下有名な話ですが
松ぼっくりのウロコ模様
ウロコ模様は螺旋を描きながら回転しています。
右回りに13列ある、螺旋は反対方向にも回転しており、左周りの螺旋は8列。
サボテンの棘も螺旋を描いている。
右回りに13列
左周りに21列
ひまわりのタネの部分にも螺旋がある。
右回りに21列
左周りに34列
また、花びらでも
ニチニチソウの花びらは5枚
クレマチスの花びらは8枚
マーガレットの花びらは21枚
こうした自然界の数を拾い出していくと、
5、8、13、21、34の数列が導き出される。
植物はこの自然界の中で進化し、進化の過程によりもっとも安定して効率的な形になり、その形がフィボナッチ数列の数となっているのではないかと考えます。
黄金比率とは
黄金比率、黄金比はどは解説するまでもなく、ご存知の方も多いかと思います。ネット上でもわかりやすいものがたくさん掲載されています。
覚えておいてほしいのは、
黄金比=1:1.618
パルテノン神殿の高さと横幅、ピラミッドの高さと底辺の長さ、など歴史的建造物やアートなど、この比率は様々なところで取り入られています。
調べるとたくさんでてきますので、ぜひ検索してみてください。人間が一番美しいと感じる比率、安定した比率と言えます。
フィボナッチ数列と黄金比の関係
フィボナッチ数列に登場する数字の 55と89 ですが、この比率は、1:1.618
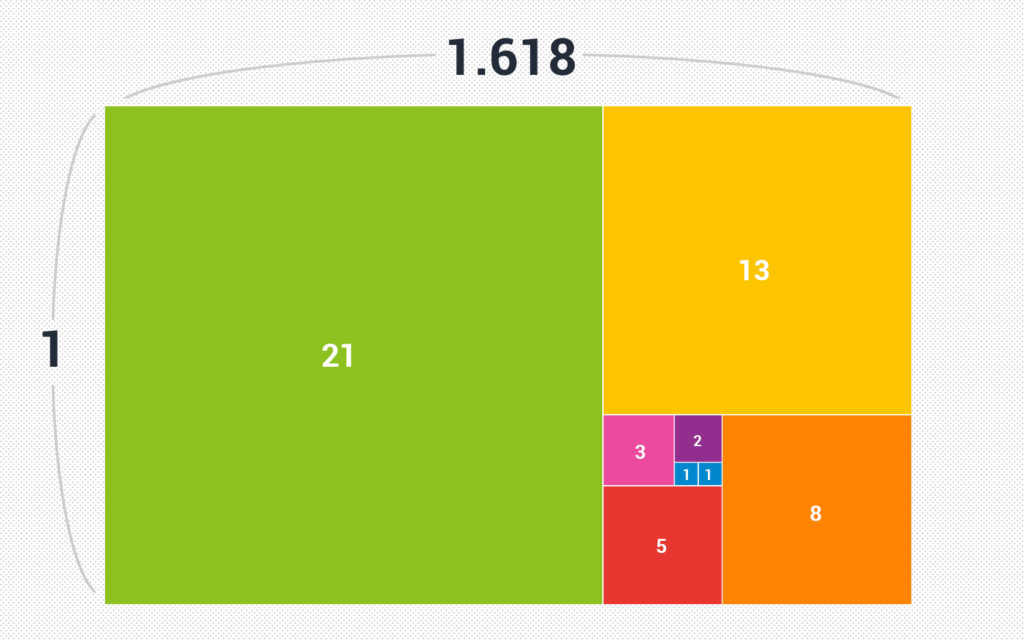
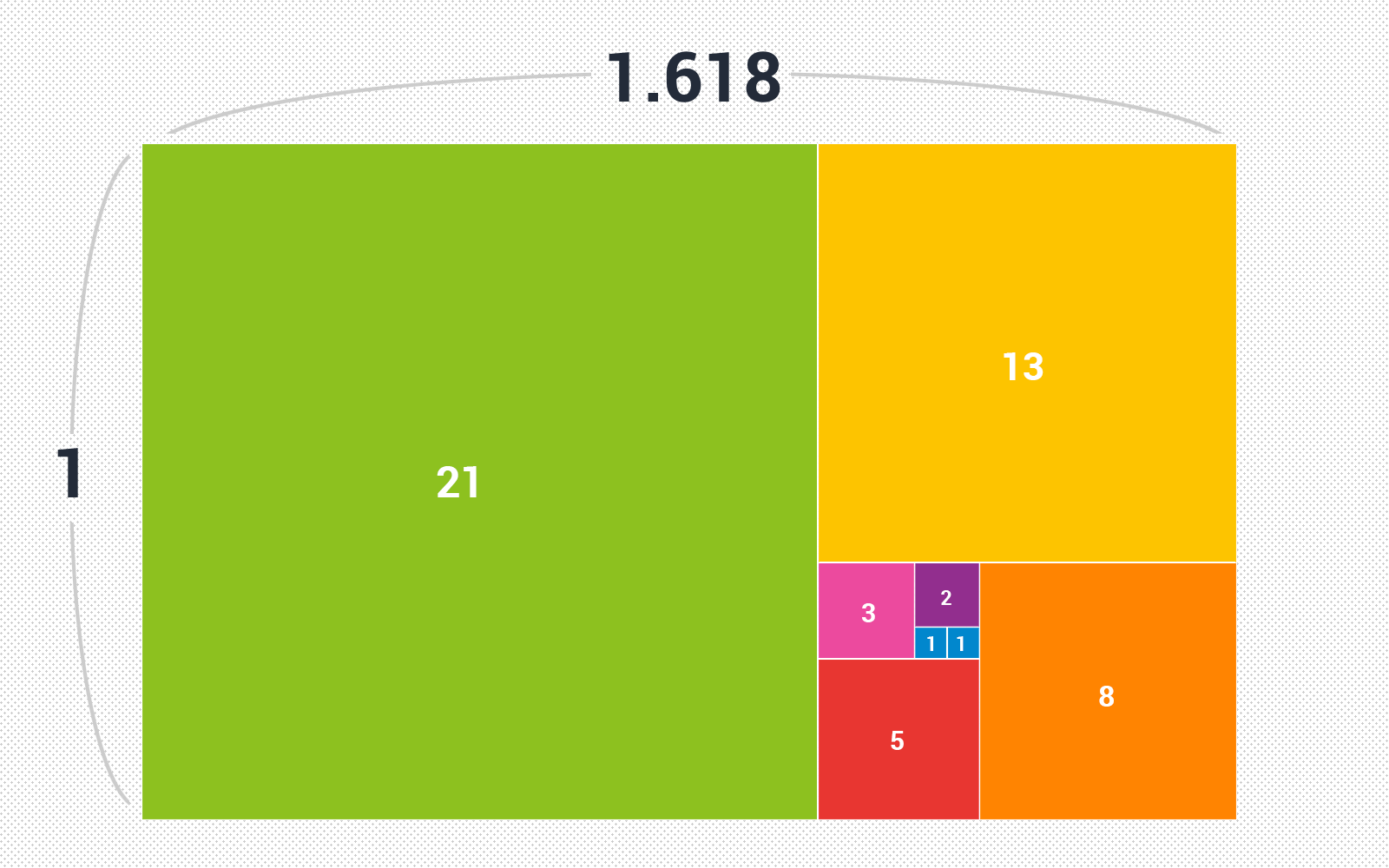
黄金比率の長方形は正方形で区切ることができます。一番小さな正方形の1辺を1とすると、各正方形の辺の長さは、1、1、2、3、5、8、13、21となります。
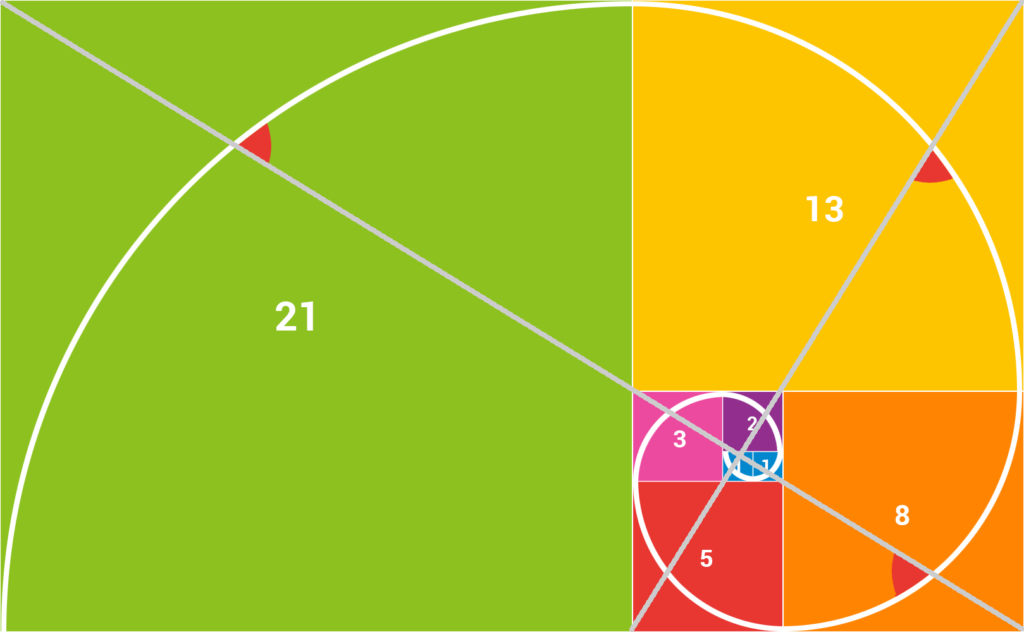
各正方形の辺の長さを半径とした曲線をつなぎ合わせると綺麗な螺旋が浮かび上がります。また、2本の対角線を引き、赤の部分の角度を見ると、角度は等しくなります。
この美しい螺旋は、オウムガイの渦巻きと同じなのは有名な話です。
このように、フィボナッチ数列と黄金比は密接に関係しており、自然界にある安定した数値、生物の進化過程の中で導かれた数値がこの黄金比率を作り上げていると言えます。
なので、黄金比は人々にとってもっとも美しい比率と感じるのではないでしょうか。
我々が美しく感じるもの、安定していると感じるもの、長く使われているものには、こうした数理的秩序が存在するものだと考えています。こうした美の原理や数理的秩序を知り、活し、人々に伝わるものや美しいと感じ取ってもらえるものを設計するのもデザイナーの大事なスキルだと考えています。



コメント